A Guided Genetic Algorithm for the Planning in Lunar Lander Games
Zhangbo Liu
Department of Computer Science
University of British Columbia
2366 Main Mall
Vancouver, B.C, V6T 1Z4, Canada
email: zephyr@cs.ubc.ca

KEYWORDS
Guided Genetic Algorithm, Reinforcement Learning,
Planning, Games
ABSTRACT
We propose a guided genetic algorithm (GA) for plan- ning in games. In guided GA, an extra reinforcement component is inserted into the evolution procedure of GA. During each evolution procedure, the reinforcement component will simulate the execution of a series of ac- tions of an individual before the real trial and adjust the series of actions according to the reinforcement thus try to improve the performance. We then apply it to a Lunar Lander game in which the falling lunar module needs to learn to land on a platform safely. We com- pare the performance of guided GA and general GA as well as Q-Learning on the game. The result shows that the guided GA could guarantee to reach the goal and achieve much higher performance than general GA and Q-Learning.
INTRODUCTION
There are two main strategies for solving reinforcement learning problems. The ¯rst is to search in the space of behaviors in order to ¯nd one that performs well in the environment. The second is to use statistical tech- niques and dynamic programming methods to estimate the utility of taking actions in states of the world (Kael- bling et al. 1996). Genetic algorithms (GA) and Tempo- ral Di®erence (TD-based) algorithms (e.g. Q-Learning) belong to each of the two categories, respectively.
Both GA and TD-based algorithms have advantages and disadvantages. GA leads to very good exploration with its large population that can be generated within a gen- eration but weak exploitation with elitism selection op- erator, because its other two operators, the crossover and mutation operators are usually randomly working. TD-based algorithms use two strategies to solve prob- lems with continuous space which are discretization and function approximation. It usually faces the curse of di- mensionality when using discretization. With function approximation it is said to be able to alleviate such a
problem but might be stuck into certain local optima. In this paper, we ¯rst investigate the GA as well as Q- Learning approach on the Lunar Lander game. Then we propose the guided GA by inserting a reinforcement component into the evolution procedure of GA. Since general GA uses random crossover and mutation opera- tions, its performance is quite unstable. Guided GA is designed to achieve higher e±ciency by involving the re- ward concept of reinforcement learning into general GA while keep all components of general GA unchanged so that the extension from general GA to guided GA is easy to achieve.
The remainder of this paper is organized as follows. In section 2 we introduce research work that is relevant to this paper. In section 3 we describe the Lunar Lander game as well as alternative approaches for the problem implemented with general GA and Q-Learning. In sec- tion 4 we present the guided GA approach for the prob- lem. The results of the experiment are shown in section 5 following by the conclusions.
RELATED WORK
Reinforcement Learning for Continuous State- Action Space Problems
The issue of using reinforcement learning to solve contin- uous state-action space problem has been investigated by many researchers. And game is actually an ideal test bed.
There are a few well known benchmark problems in the reinforcement learning domain such as Mountain Car (Moore and Atkeson 1995), Cart-Pole (Barto et al. 1983) and Acrobot (Boone 1997). In the Mountain Car prob- lem, the car must reach the top of the hill as fast as possible and stop there. This problem is of dimension 2, the variables being the position and velocity of the car. The Cart-Pole is a 4-dimensional physical system in which the cart has to go from the start point to the goal and keep the orientation of its pole vertical within a certain threshold when it reaches the goal. The Acrobot problem is also a 4-dimensional problem which consists of a two-link arm with one single actuator at the elbow. The goal of the controller is to balance the Acrobot at

its unstable, inverted vertical position, in the minimum time. Another implementation described in (Ng et al. 2004) made an autonomous inverted helicopter °ight.
Two main strategies here are discretization and func- tion approximation. For the ¯rst strategy, discretization techniques have been widely pursued and provide con- vergence results and rates of convergence (Munos and Moore 2002), (Monson et al. 2004). For the second strategy, several approaches come out on how to con¯g- ure with multiple function approximators (Gaskett et al. 1999), (Smart and Kaelbling 2000).
Reinforcement Learning + Genetic Algorithm
Some researches on combining the advantages of GA and TD-based reinforcement learning have been proposed in (Chiang et al. 1997), (Lin and Jou 1999). However, both of them use gradient decent learning method which is complex and the learning speed is always too slow to achieve the optimum solution. The idea of guided GA we propose is inspired by (Ito and Matsuno 2002), in which Q-Learning is carried out and ¯tness of the genes is calculated from the reinforcedQ-table. However, in guided GA, instead of usingQ-table, we directly insert a reinforcement component into the evolution procedure of the general GA so that the large Q-table and hid- den state problem are avoided. In (Juang 2005), Juang proposed another approach to combine online clustering and Q-value based GA for reinforcement fuzzy system design. Compared with the approach described in that paper, guided GA is much simpler in structure and eas- ier to implement while the problem we address in this paper has a higher dimension than that of in (Juang 2005).
THE LUNAR LANDER GAME
The Lunar Lander Game
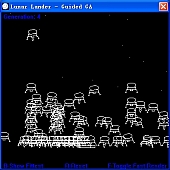
The Lunar Lander game is actually a physically-based problem in which the controller needs to gently guide and land a lunar module onto a small landing platform, as shown in Figure 1. The space is a 400 £ 300 pixel rectangle area. It simulates the real environment on the moon that the lunar module has mass and is in°uenced by the gravity on the moon (1.63m/s2). The controller here has 5-dimensional state spaces which are: position (x; y), velocity (x; y) and orientation (µ). The controller is able to do four actions: rotate left, rotate right, thrust and do nothing (drift).
When agent becomes the controller instead human player, the problem becomes to an advanced path ¯nd- ing issue. The successful landing requirement consists the checking of the following variables when any part of the lunar module reach the ground:
² Distance from the pad
Figure 1: The Lunar Lander Game
²Speed
²Degrees of rotation
All of them must be below certain thresholds to achieve safe landing, otherwise it will crash and the game will start from beginning again. The game runs in real time thus it is a good test bed for problems with continuous state and discrete action spaces.
Alternative Approaches
Genetic Algorithm
One alternative approach to this problem is using ge- netic algorithm (GA) for planning. For a complete in- troduction to GA please refer to (Goldberg 1989). The GA approach to this problem follows the steps below in one epoch to try to achieve the goal.
First, the genome is encoded as a series of genes each of which contains an action-duration pair, as shown in Figure 2. The duration here represents the period of time that each speci¯c action is applied. At the begin- ning, all the actions and durations in those genes in one genome are randomly assigned. A number of genomes will be created together in one generation.
Figure 2: Genome encoding
Next, the controller starts a trial according to theaction-duration series in each genome and uses a ¯t- ness function to evaluate their utilities when they crash. There might be many approaches to build the ¯tness

function to this problem. In (Buckland and LaMothe 2002), Buckland and LaMothe suggested the following ¯tness function:
Fitness = w1 ¢ disFit + w2 ¢ rotFit + w3 ¢ airTime (1)
where disFit and rotFit represent the value function of the position and the orientation feature separately. TheairTime is the time period that the lunar module stays in the air which is de¯ned as na=(v + 1) where na is the number of actions it does ignoring the duration and v is the velocity at landing. wi are the weights that are applied to balance the function. Those weights are quite important and must be carefully decided in order to achieve a good performance. If the safe landing re- quirement is satis¯ed, the ¯tness value will be assigned with a prede¯ned Big Number instead of calculating using the equation (1).
After one trial for all genomes of the current generation, the ¯tness value of each genome will be calculated out and the best n genomes with the highest ¯tness value will remain and put into the next generation. Other genomes of the next generation are created by using crossover and mutation operators. The crossover opera- tor works by stepping through each gene in its parents' genome and swapping them at random to generate their o®spring. The mutation operator runs down the length of a genome and alters the genes in both action and duration according to the mutation rate.
The operator will periodically do one epoch after an- other until one genome's result reaches the goal or the number of generations exceeds the prede¯ned maximum value. An implementation of a GA solution to this prob- lem can be found in (Buckland and LaMothe 2002).
Based on our experience, Q-Learning with only dis- cretization won't work for this problem. So we im- plement a linear, gradient-descent version of Watkins's Q(¸) to this problem with binary features, "-greedy pol- icy, and accumulating traces described in (Sutton and Barto 1998). Tile coding (Sutton and Barto 1998) is also used to partition the continuous space into multi- ple tilings.
THE GUIDED GENETIC ALGORITHM AP- PROACH
The approaches we mentioned in the previous section both have advantages and disadvantages. The GA is simple to implement and is able to achieve the goal, while its disadvantage is that all its actions are randomly assigned so that its performance is quite unstable. The basic concept of Q-Learning approach is also simple and supposed to be e±cient. However, for this game which is a realtimecontinuous-state problem, Q-Learning with
discretization does not work and Q-Learning with func- tion approximation is hard to accommodate. We design the guided GA which incorporates the concept of reward in Q-Learning into GA. Here we call our function "rein- forcement function" because unlike the reward function in Q-Learning whose values need to be summed to cal- culate the Q-value (Q = Prewards), the reinforcement function here gets the immediate ¯tness value and will be extended to ¯tness function at the end of each epoch. In the following subsections we ¯rst introduce the rein- forcement function design for guided GA to this problem then discuss the details of the algorithm.
Reinforcement Function Design
To model the reinforcement function is a very challeng- ing work. It has to be smoothly transformed to the ¯tness function of the general GA (equation (1)) at the end of each epoch so that we can easily extend the gen- eral GA to a guided GA without modifying the existing ¯tness function. On the other hand, it should be prop- erly de¯ned to e±ciently guide the agents to perform better. We tried many di®erent versions until ¯nally reaching a solution.
In equation (1) there are 3 parameters and we need to modify two of them which are disFit and airTime in our reward function. The main di®erence between equation
(1) and the reinforcement function is that in equation (1), all lunar modules reach the ground (position:y = 0) and each of them has an accumulator na whose value is the number of actions they do during the whole pro- cedure; while in the reinforcement function, the lunar modules are in the air and they only focus on the next action. Based on this di®erence, we build our reinforce- ment function as follows:
We use disFitx to represent disFit in (1), then we builddisFity which is similar to disFitx but for y coordinate. Then our distance function is:
disFit0 = s(disFitx)2 +
|
(
|
disFity)2
|
(2)
|
wy
|
where wy is used for balancing the weight betweendisFitx and disFity.
airTime, as mentioned in equation (1), is de¯ned as na=(v + 1). In our reinforcement function, na no longer exists, while we ¯nd that a single de¯ned function does not work well all the time since on di®erent stages our focuses might be di®erent. For example, when the lunar module is high in the air we would pay more attention on its horizontal position; while when it is close to the ground it needs to slow down to prepare for landing. So instead of simply rede¯ning it as 1=(v + 1), we take the vertical position into consideration and come with the following de¯nition:
n¤ De¯ning disFit0 and airTime0 ¤n
if position:y < h1f disFit0 = disFit0 £ r; ifposition:y < h2
airTime0 = 1=(wt £ v + 1); gelse airTime0 = 1=(v + 1);
where h1 and h2 (h1 > h2) are values of height at which we think should change our strategies and wt is the weight that can help slow down the velocity of the lunar module to very small values when they nearly reach the ground. r is a scaling factor. Then the reward function we build is:
R = w1 ¢ disFit0 + w2 ¢ rotFit + w3 ¢ airTime0 (3)
where wi and rotFit are the same as in (1).
Algorithm Description
In each epoch of the GA, the evolution of its genomes is done by three operators: selection, crossover and mu- tation. The selection is based on elitism, while the crossover and mutation are by random, which leads to the unstable performance of the general GA. In order to better perform the evolution, we insert a reinforce- ment component whose idea comes from the reward in Q-Learning. There are two strategies to do this. The ¯rst one is on-line updating which is similar to other reinforcement learning algorithms. The second one is o®-line updating which updates the whole genome at one time before each epoch. We choose the latter based on the consideration of both the standard mechanism of GA and the real time property of the problem. The high-level description of the guided GA is shown below:
algorithm guided genetic; begin
obtain last generation;
put a few best individuals directly into new generation;
use crossover operator to generate new generation; use mutate operator on the new generation; evolve the new generation;
end
What we add here is the last step whose input is the mutated new generation. Below is the procedure:
procedure evolve; begin
for each individual i in the generation
for each gene in i's action-duration series get duration d, current state s;
from state s consider all possible actionsa0i with duration d, suppose s0i are possible resulting states;
select a0 and s0 based on equation (3);
if s0 satis¯es safe landing requirement
aà a0; else if a0 =6 a
aà a0 with probability (1 ¡ "); update state;
end
where the greedy rate " has the same meaning as the"- greedy policy in reinforcement learning. For any given gene of an individual's genome, there are 4 possible ac- tions and numerous durations (in our implementation for the problem the duration ranges from 1 to 30, which means for any given state there are 120 possible states in the next step). And we would only change the action in action-duration pair so that for any given state there are only 4 possible states in the next step.
We use the "-greedy policy here, but unlike the so called greedy genetic algorithm (Ahuja et al. 1995) which fo- cuses on greedy crossover, guided GA is inspired by (Ito and Matsuno 2002) in which the authors used Q-table to integrate Q-Learning with GA. However, for our prob- lem using Q-table won't work because of the large state space. Instead, we use the above method to directly insert the reinforcement component into the evolution procedure without saving any previous state or function value in the memory.
EXPERIMENTAL DETAILS
Experimental Design and Results
We conducted an experiment to test the performance of our guided GA and compared it with the general GA and Q-Learning. For guided GA and general GA, we made all variables the same for both of them to ensure fairness. The parameters of our experiment were given as follows:
1.Both of the two contained 100 individuals in one generation. The maximum number of generations was 500. It supposes to be failed if it did not achieve the goal within 500 generations and then would start from the beginning again. The length of chromosome was 50. The crossover rate was 0.7 and the mutation rate was 0.05. The " was 0.1.
2.The thresholds for the safe landing requirements were:
(a)Distance = 10.0
(b)Velocity = 0.5
(c)Rotation = ¼/16
3.To de¯ne the values of weights was the most di±- cult work for the experiment. Below are the best value settings that were selected by empirical study:
(a)w1 = 1; w2 = 400; w3 = 4 (got from (Buckland and LaMothe 2002))

(b) wy = 3; wt = 6; r = 1:7; h1 = 100; h2 = 30
We also introduced the same feature of guided GA toQ-Learning implementation for building its reward func- tion.
To learn to solve a problem by reinforcement learning, the learning agent must achieve the goal (by trial-and- error) at least once (Lin 1992). Testing results showed that general and guided GA were able to achieve the goal almost every time. However, it was very hard forQ-Learning to complete the task. Besides the general reasons such as function approximation strategy often falls into local optimal and Q-Learning converges too slowly, we believed that another important reason was in this realtime problem the control of duration of the action is crucial. GAs could evolve the durations with the crossover and mutation operation. But Q-Learning could not. Adding duration together with action into the state space might make the state space extremely huge, thus lead to Q-Learning's fail. Based on this fact, we only compared the data we got from the testings using general GA and guided GA. The experimental re- sults that we ran both of general and guided GA for 25 trials are shown in Figure 3.
Figure 3: Experimental Results
From the results we can observe that for most of the time the performance of the guided GA were much higher than the general GA except the last trial. Figure 4 shows the ¯tness that both of them gained during all the generations before the last generation in the 13th trial. According to the data, both the highest and the average ¯tness of guided GA were higher than general GA.
Analysis
Some questions came out when we observed the data of the results. First, what was the goal's ¯t- ness/reinforcement value? Second, why the highest ¯t- ness of guided GA was much higher than that of general GA while they achieved the goal in very close steps? Third, why guided GA lost in the last trial while per- formed much better in previous trials?
Figure 4: Fitness Gained in the 13th Trial
We used the thresholds for the problem to calculate out the ¯tness value and found that the ¯tness value of the goal was just no more than 900. The reason why those individuals with very high ¯tness values failed to achieve the goal was that there were three parameters in the ¯tness/reinforcement function. No matter how high the ¯tness value that certain individual gained, as long as there was one parameter whose value was above the threshold then it failed to achieve the goal. So it was possible that one individual with a low ¯tness achieved the goal in the next generation by randomly evolving its genome which accidentally hit all the thresholds and triggered a sudden success. And that was the reason that sometimes the individual who achieved the goal was not the one who performed the best in the previous state.
Both general and guided GA involved randomness that brought the uncertainty to the procedure. So the possi- ble explanation to the third question was that the ran- domness caused a sudden success to the general GA before the guided GA got out of certain local optimal states.
Although the highest ¯tness in each step did not make much sense to us, the average ¯tness were useful because higher average ¯tness demonstrated a better chance for the whole generation to achieve the goal. For all the trials we observed, the average ¯tness of guided GA were much higher than the average ¯tness of general GA.
CONCLUSION AND FUTURE WORK
In this paper we proposed a guided genetic algorithm by adding a reinforcement component into GA. We success- fully applied the guided GA for the planning of Lunar Lander game. Based on the experimental results, guided GA achieved much higher performance than general GA and Q-Learning.
The guided GA which we proposed in this paper demon- strated very good performance. However, it still has some shortcomings and has the potential to be im- proved. Possible improvement direction are: ¯rst, ¯gure out a method that could update the reinforcement func- tion more e®ectively; second, optimize the procedure of
crossover and mutation; last but not the least, ¯nd out some rules to model the reinforcement function without doing trial-and-error.
ACKNOWLEDGEMENT
We would thank Dr. David Poole, Dr. Michiel van de Panne, Dr. Chris Gaskett and Joel Lanir for their invaluable suggestions on our work. We also appreciate peer reviewers for their precious comments.
REFERENCES
R. Ahuja, J. Orlin, and A. Tivari. A greedy genetic algo- rithm for the quadratic assignment problem. Working pa- per 3826-95, Sloan School of Management, MIT, 1995.
A.G. Barto, R.S. Sutton, and C.W Anderson. Neurolike adaptive elements that can learn di±cult control prob- lems. IEEE. Trans. on System Man and Cybernetics, 1983.
G. Boone. Minimum-time control of the acrobot. Interna- tional Conference on Robotics and Automation, 1997.
M. Buckland and A. LaMothe. AI techniques for game pro- gramming. Premier Press, 2002.
C.K. Chiang, H. Y. Chung, and J. J. Lin. A self-learning fuzzy logic controller using genetic algorithms with rein- forcements. IEEE Transactions on Fuzzy Systems, 1997.
C. Gaskett, D. Wettergreen, and A. Zelinsky. Q-learning in continuous state and action spaces. In Australian Joint Conference on Arti¯cial Intelligence, pages 417{428, 1999.
D.E. Goldberg. Genetic Algorithm in Search, Optimiza- tion and Machine Learning. Kluwer Academic Publishers, 1989.
K. Ito and F. Matsuno. A study of reinforcement learning for the robot with many degrees of freedom - acquisition of locomotion patterns for multi-legged robot. In ICRA '02. IEEE International Conference on Robotics and Au- tomation, pages (4):3392{3397, 2002.
C.F. Juang. Combination of online clustering and q-value based ga for reinforcement fuzzy system design. IEEE Transaction on Fuzzy Systems, 2005.
L.P. Kaelbling, M.L. Littman, and A.P. Moore. Reinforce- ment learning: A survey. Journal of Arti¯cial Intelligence Research, 4:237{285, 1996.
C.T. Lin and C.P. Jou. Controlling chaos by ga-based rein- forcement learning neural network. IEEE Transaction on Neural Networks, 1999.
L.J. Lin. Self-improving reactive agents based on reinforce- ment learning, planning and teaching. Mach. Learn., 8(3-4):293{321, 1992.
C.K. Monson, D. Wingate, K.D. Seppi, and T.S. Peterson. Variable resolution discretization in the joint space. In- ternational Conference on Machine Learning and Appli- cations, 2004.
A.W. Moore and C.G. Atkeson. The parti-game algorithm for variable resolution reinforcement learning in multi- dimensional state-spaces. Mach. Learn., 21(3):199{233, 1995.
R. Munos and Andrew Moore. Variable resolution discretiza- tion in optimal control. Mach. Learn.,49(2-3):291{323, 2002.
A.Y. Ng, A. Coates, M. Diel, V. Ganapathi, J. Schulte, B. Tse, E. Berger, and E. Liang. Inverted autonomous helicopter °ight via reinforcement learning, 2004.
W.D. Smart and L.P. Kaelbling. Practical reinforcement learning in continuous spaces. In Proc. 17th International Conf. on Machine Learning, pages 903{910. Morgan Kauf- mann, San Francisco, CA, 2000.
R.S. Sutton and A.G. Barto. Reinforcement Learning: An Introduction. Number 206-214. MIT Press, Cambridge, MA, 1998.
BIOGRAPHY
ZHANGBO LIU studies computer science at the Univer- sity of British Columbia, Canada. His main research in- terests are human-computer interaction and arti¯cial intelli- gence in games.






